PLASIMO's fluid models use advanced methods to calculate the transport coefficients of mixtures. The calculations rely on the Chapman-Enskog expansion. This method is used to calculate the electrical conductivity, the thermal conductivity and the viscosity. PLASIMO also contains accurate approximations for binary interactions and for thermodynamic identities.
For the electrical conductivity Devoto's second order expression [1, eq. 16] is used. It calculates the conductivity by only including the contribution from the electrons. The contribution from the ions is neglected as they are significantly less mobile. The thermal conductivity is calculated as the sum of the translational, the reactive and the internal contributions as
\begin{equation} \lambda = \lambda_{\mathrm{hp}} + \lambda_{\mathrm{e}} + \lambda_{\mathrm{r}} + \lambda_{\mathrm{int}} \end{equation}The translational contributions of the heavy particles is calculated according to the second order expression from Muckenfuss and Curtiss [2]. The translational contribution from the electrons is evaluated using Devoto's third order expression [1, eq. 21]. The fact that these two translational contributions are separated makes the implementation valid for both LTE and non-LTE plasmas (that can be described by the fluid approximation). The last two terms, the reactive and internal thermal conductivity, are specific for LTE plasmas. These terms account for the transfer of energy corresponding to chemical energy and excited states. In non-LTE plasmas these terms are included separately in the energy balance. The reactive thermal conductivity is calculated according to Butler and Brokaw [3, eq. 3]. The internal contribution is based on Euckens approximation [4, p. 22,274]. The viscosity is included by only considering the contribution from the heavy particles [5, p. 531-532]. The first order approximation is used. For more details on the calculation procedure and the validity of the expansion, see [6, p. 91-100].
The calculated transport properties have been verified by using the planetary atmospheres described by Capitelli et al [4, ch. 11]. These atmospheres are the Jupiter (\(x_{\mathrm{H_2}}\) = 0.89 and \(x_{\mathrm{He}}\) = 0.11), air (\(x_{\mathrm{N_2}}\) = 0.8 and \(x_{\mathrm{O_2}}\) = 0.2) and Mars (\(x_{\mathrm{CO_2}}\) = 0.953, \(x_{\mathrm{N_2}}\) = 0.027, \(x_{\mathrm{Ar}}\) = 0.016 and \(x_{\mathrm{O_2}}\) = 0.004) atmospheres. Additionally, a comparison is made with a pure argon plasma calculated by Murphy [7]. All of these plasmas are evaluated under LTE conditions, since this provides a mixture reference that is independent of chemical reactions. As indicated above, due to the separation of the electron and heavy particle terms, the benchmark is also valid for non-thermal plasmas. Due to the usage of LTE for the benchmark, PLASIMO now also contains accurate descriptions of the partition sums of the particles that are involved in the mentioned planetary atmospheres. Accurate thermodynamic quantities are therefore also available. These include the entropy, internal energy, enthalpy, Helmholtz free energy, Gibbs free energy and the specific heat.
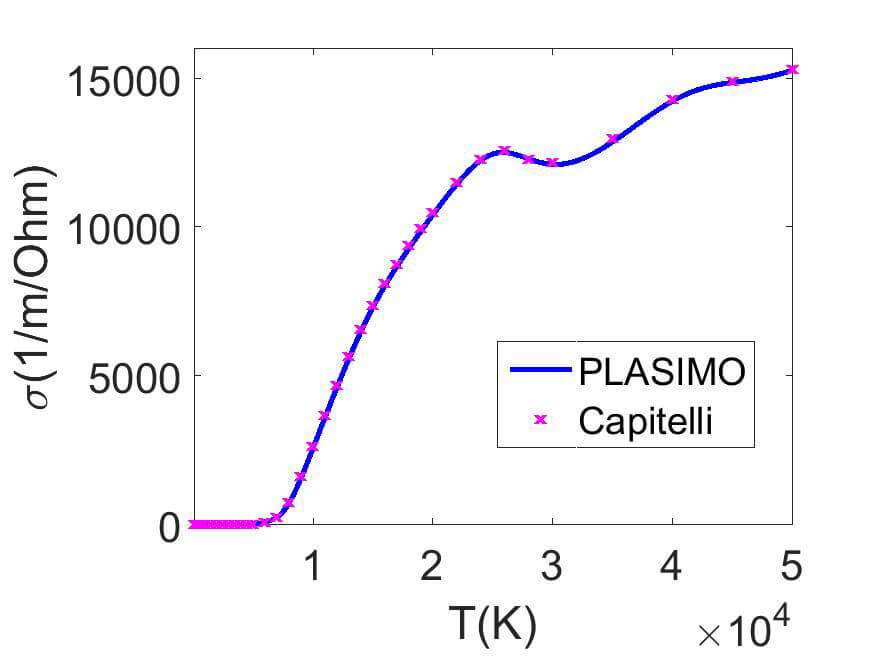
(a) Air
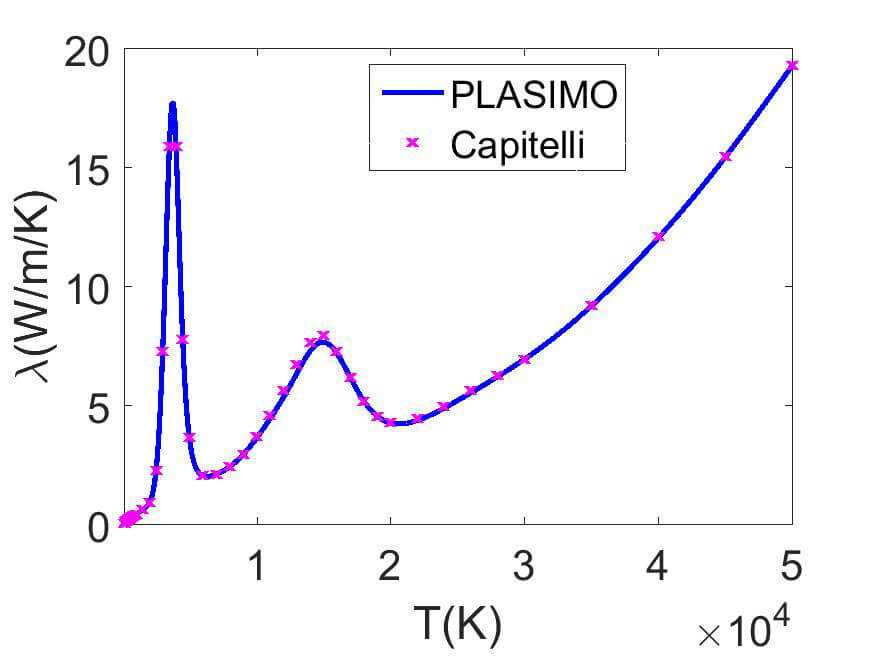
(b) Jupiter
A comparison is made in figure 1 between the result of Capitelli et al and the PLASIMO results for the electrical conductivity in air and the thermal conductivity in the Jupiter atmosphere.
The electrical conductivity initially increases due to the increasing ionization degree. After that the density decreases again due to the ideal gas law. At the temperature where double ionization takes place another small peak can be observed.
The thermal conductivity of the Jupiter atmosphere contains two peaks that are related to the dissociation of H2 and the ionization of H. The small ionization peak of He is not visible. The overall increasing trend is related to the thermal conductivity of the electrons.
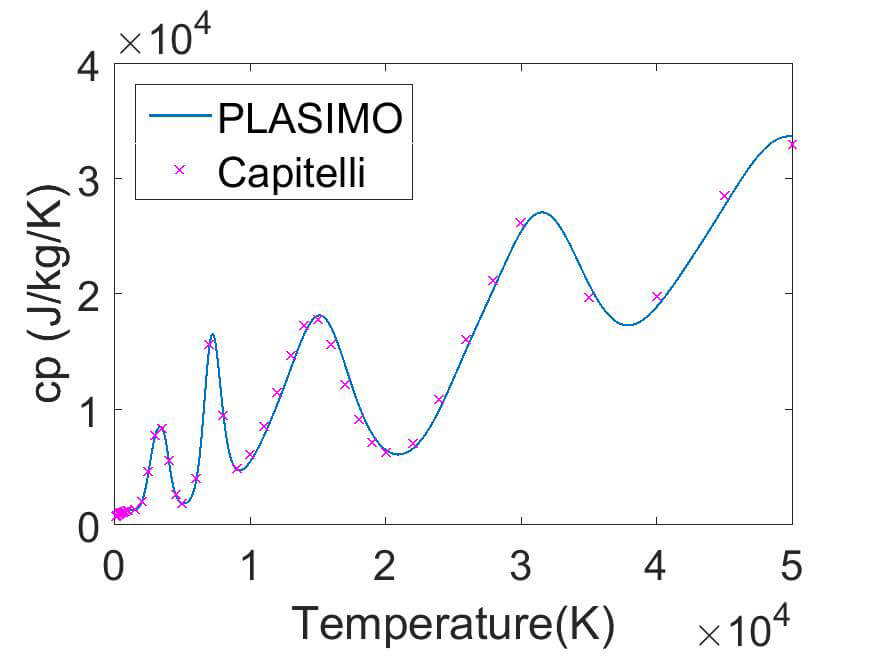
(c) Mars
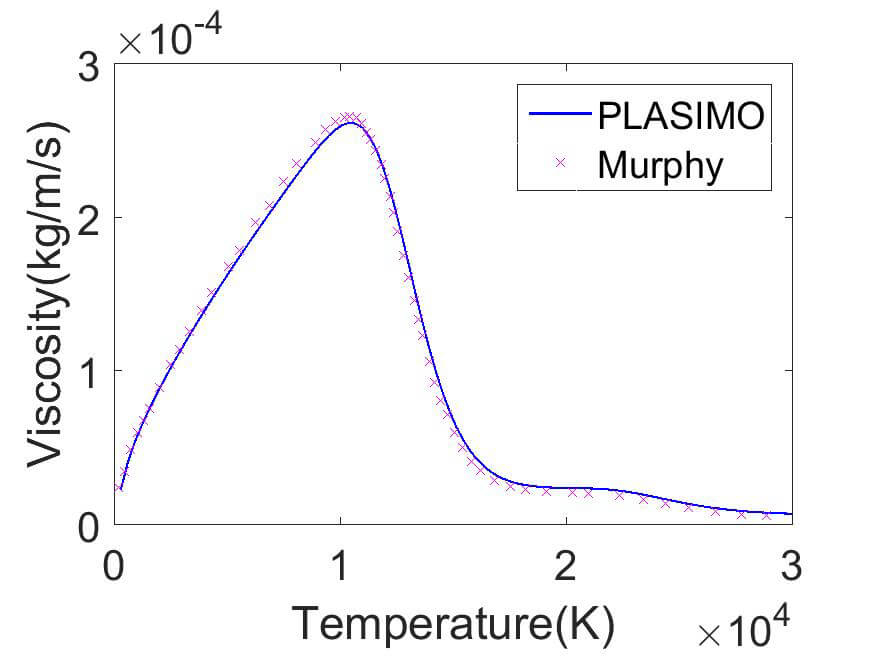
(d) Argon
In figure 2 the PLASIMO results are compared to the result of Capitelli et al for the specific heat in Mars and to Murphy for the viscosity in pure argon.
The specific heat for the Mars atmosphere shows the peaks that correspond to the dissociation of CO2 to CO, the dissociation to C and O. The last peaks correspond to the first till the third ionization stage. Where the third peak is not fully resolved.
The viscosity of argon initially increases with temperature. Since the ion-ion and resonant ion-neutral cross sections are significantly larger than the neutral-neutral interactions, the viscosity drops to lower values when the ionization degree becomes significant. A second decrease can be observed when the ions become doubly ionized.
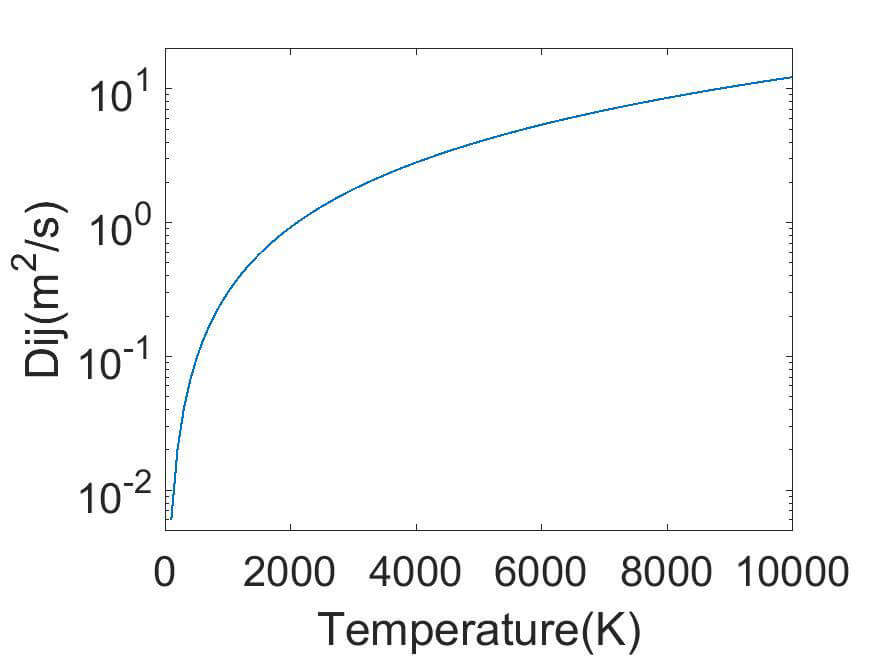
(e) Diffusion coefficient for O2+ in O2
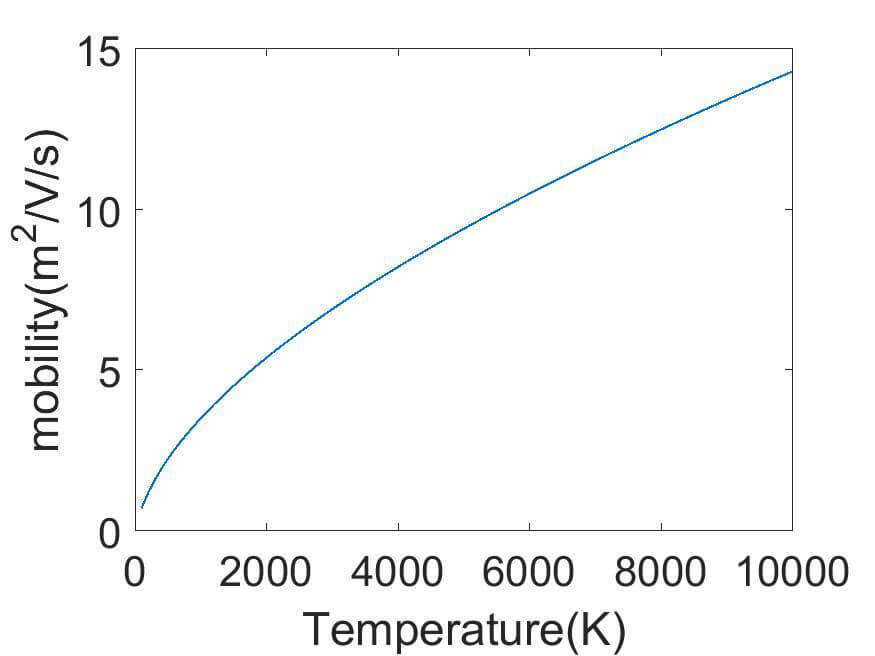
(f) Mobility for 02+ in O2
The previous calculations all accounted for a transport coefficient that corresponds to the entire mixture. The necessary ingredients for these calculations are the collision integrals for binary interactions. Binary interactions for neutral-neutral and neutral-ion interactions are described according to the generalized Lennard Jones potential [8]. The potential parameters are estimated based on the polarizability of the individual species. For neutral-ion interactions of the type A - A+ an additional contribution related to charge-exchange is taken into account. It is calculated according to Rapp and Francis [9]. Neutral-electron interactions are included via electron momentum transfer cross sections when available. Otherwise the Langevin potential is used. The charged-charged interactions are included via the screened Coulomb potential [10, 11].
The collision integrals can be used to calculate diffusion coefficients and mobilities. The mobility is derived from the diffusion coefficient by using the Einstein relation. Examples of such calculations are shown in figure 3 for O2 and O2+ for a pressure of 10 Pa.
References
[1] R. S. Devoto. Simplified expressions for the transport properties of ionized monatomic gases. Phys. of Fluids, 10(10), 2105, 1967.
[2] C. Muckenfuss and C. F. Curtiss. Thermal conductivity of multicomponent gas mixtures. J. Chem. Phys., 29, 1273, 1958.
[3] Richard S. Brokaw. Thermal conductivity of gas mixtures in chemical equilibrium. ii. The Journal of Chemical Physics, 32(4), 1005-1006, 1960.
[4] M. Capitelli, D. Bruno, and A. Laricchiuta. Fundamental aspects of plasma chemical physics. Transport. Springer, 2013.
[5] J. O. Hirschfelder, C. F. Curtiss, and R. B. Bird, editors. Molecular Theory of Gases and Liquids. (New York: Wiley & Sons), 1964.
[6] J. F. J. Janssen. Equilibrium and Transport in Molecular Plasmas. PhD thesis, Eindhoven University of Technology, The Netherlands, 2016.
[7] A. B. Murphy. Transport coefficients of air, argon-air, nitrogen-air,and oxygen-air plasmas. Plasma Chemistry and Plasma Processing, 15(2), 279–307, 1995.
[8] A. Laricchiuta, G. Colonna, D. Bruno, R. Celiberto, C. Gorse, F. Pirani, and M. Capitelli. Classical transport collision integrals for a lennard-jones like phenomenological model potential. Chem. Phys. Let., 445, 133–139, 2007.
[9] Donald Rapp and W. E. Francis. Charge exchange between gaseous ions and atoms. The Journal of Chemical Physics, 37(11), 2631–2645, 1962.
[10] E. A. Mason, R. J. Munn, and Francis J. Smith. Transport coefficients of ionized gases. Physics of Fluids, 10(8), 1827–1832, 1967.
[11]R. S. Devoto. Transport coefficients of ionized argon. Physics of Fluids (1958-1988), 16(5), 616–623, 1973.