In order to predict the spectrum of a plasma the equation of radiative transport must be solved. It is given by
\begin{equation} \frac{dI_\nu}{ds}=j_\nu - \kappa_\nu I_\nu \end{equation}where \(I_\nu\) is the spectral radiance in units of W m-2sr-1Hz-1, \(j_\nu\) the emission in units of W m-3sr-1Hz-1, \(\kappa\) the absorption in m-1 and \(s\) the path traversed by the radiation. From this equation it is apparent that radiation transport is a non-local problem. Radiation emitted at a specific location can be absorbed at a completely different location. This for example occurs in the atmosphere of the earth where the solar radiation is partly absorbed.
In order to account for this non-local nature, the raytracing method is used. This method selects a point on the wall of a numerical cell and divides the solid angle in several sections. Each section is represented by a single ray as depicted in figure 1 for the outer two shells.
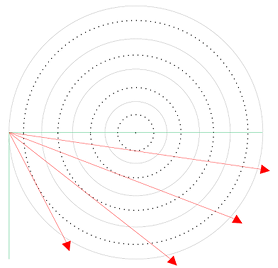
(a) outer shell
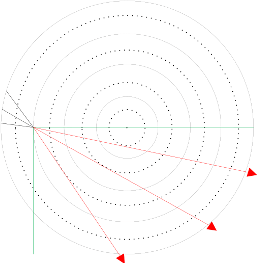
(b) second shell
Figure 1: Numerical mesh used for the raytracing method.
For specific geometries, like a cylinder or a sphere, and using azimuthal symmetry it is possible to capture the energy transfer due to radiation with a limited amount of rays. By rotating the rays in azimuthal direction the discretization for the outer shells can be depicted as shown in figure 2.
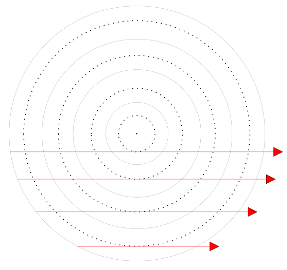
(a) shifted outer shell
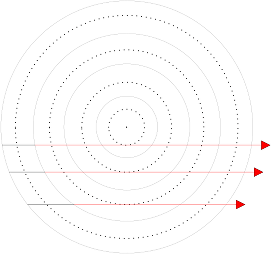
(b) shifted second shell
Figure 2: Numerical mesh used for the raytracing method.
After rotating the rays it is apparent that the rays corresponding to the outer two shells use the same discretization. Due to this discretization it is possible to capture to the energy transport efficiently. In more complex geometries symmetry considerations are not always possible and the method can become rather time consuming. It is recommended to apply raytracing in geometries where it is possible to apply symmetry.
The equation of radiative transport is solved analytically within one cell where \(j_\nu\) and \(\kappa_\nu\) are assumed to be constant. The new value for \(I_\nu\) is given to the neighboring cell as input. This procedure is followed until the boundary of the domain is reached. The result of such a calculation for a metal halide lamp with InI filling is given in the figure below.
![[ spectrum XeInI ]](../../images/modules/radiation-transport/spectral_video_XeInI_C17_mass_1200nm.gif)
The evolution of the spectral radiance as a function of the radial position in the plasma.
![[ arrow ]](../../images/modules/radiation-transport/animated_arrow.gif)
Typical for high pressure plasmas is that part of the radiation reaches thermal conditions. For radiation that means that parts of the spectrum can be modeled with a blackbody radiator. This is for example the case for the UV part of the spectrum which rises towards a peak value in the core of the plasma. On the way out of the plasma practically all UV radiation is absorbed. Since the visible and infrared radiation is not in equilibrium it can escape from the plasma without significant absorption. More information can be found in [1].
References
[1] J.F.J. Janssen. Equilibrium and Transport in Molecular Plasmas. PhD thesis, Eindhoven University of Technology, The Netherlands, 2016.